Tutorial: Maps in the BGG complex

This page appears both rendered to HTML in the docs, and as an interactive notebook in the /examples folder in the repository.

from bggcohomology.bggcomplex import BGGComplex

Using this code we can display the BGG complex as a graph, and describe all the maps in the complex. Shown here is the Bruhat graph for \(G2\). The vertices are enumerated by elements of the Weyl group, represented by a reduced word in simple reflections. That is, e.g. "12" denotes the product \(s_1s_2\), with \(s_i\) the \(i\)th simple reflection. Notice that the vertices are color coded by column number / word length of the Weyl group element \(\ell(w)\). There is an edge \(x\to y\) if and only if there is a relection \(t\in W\) such that \(y=tx\) and \(\ell(y)=\ell(x+1)\).

d = 'G2'
BGG = BGGComplex(d)
BGG.plot_graph()

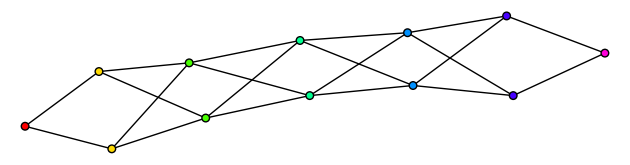
We can list all the edges in the Bruhat graph like this:

BGG.arrows

[('', '1'),
 ('', '2'),
 ('2', '12'),
 ('2', '21'),
 ('1', '21'),
 ('1', '12'),
 ('12', '212'),
 ('12', '121'),
 ('21', '121'),
 ('21', '212'),
 ('121', '2121'),
 ('121', '1212'),
 ('212', '1212'),
 ('212', '2121'),
 ('2121', '12121'),
 ('2121', '21212'),
 ('1212', '21212'),
 ('1212', '12121'),
 ('21212', '212121'),
 ('12121', '212121')]

Now suppose we want to look at the BGG complex associated to some weight \(\mu\), for example the weight \(\mu=0\). This associates to each edge \((x,y)\) an element \(\mathcal F(x,y)\in U(\mathfrak n)\). These maps satisfy that for each ‘square’ \(w\to x\to w'\), \(w\to y\to w'\) we have \(\mathcal F(w,x)\mathcal F(x,w')=\mathcal F(w,y)\mathcal F (y,w')\).

We can run the following code:

BGG.display_maps((0,0))

$$\to1,\,\,\,f_{1}$$

$$\to2,\,\,\,f_{2}$$

$$1\to12,\,\,12\,f_{2111} -4\,f_{1}\,f_{112} +4\,f_{1}^{2}\,f_{12} +\,f_{2}\,f_{1}^{3}$$

$$1\to21,\,\,\,f_{2}^{2}$$

$$2\to12,\,\,\,f_{1}^{4}$$

$$2\to21,\,\,-\,f_{12} +\,f_{2}\,f_{1}$$

$$12\to121,\,\,2\,f_{112} +4\,f_{1}\,f_{12} +\,f_{2}\,f_{1}^{2}$$

$$12\to212,\,\,\,f_{2}^{3}$$

$$21\to121,\,\,\,f_{1}^{5}$$

$$21\to212,\,\,-12\,f_{12}\,f_{112} +2\,f_{1}\,f_{12}^{2} +8\,f_{2}\,f_{1}\,f_{112} -2\,f_{2}\,f_{1}^{2}\,f_{12} +\,f_{2}^{2}\,f_{1}^{3}$$

$$121\to1212,\,\,-12\,f_{12}\,f_{112} +12\,f_{1}\,f_{12}^{2} -12\,f_{2}\,f_{1}\,f_{112} +8\,f_{2}\,f_{1}^{2}\,f_{12} +\,f_{2}^{2}\,f_{1}^{3}$$

$$121\to2121,\,\,\,f_{2}^{3}$$

$$212\to1212,\,\,\,f_{1}^{5}$$

$$212\to2121,\,\,8\,f_{112} -2\,f_{1}\,f_{12} +\,f_{2}\,f_{1}^{2}$$

$$1212\to12121,\,\,2\,f_{12} +\,f_{2}\,f_{1}$$

$$1212\to21212,\,\,\,f_{2}^{2}$$

$$2121\to12121,\,\,\,f_{1}^{4}$$

$$2121\to21212,\,\,-18\,f_{2111} +6\,f_{1}\,f_{112} -\,f_{1}^{2}\,f_{12} +\,f_{2}\,f_{1}^{3}$$

$$12121\to212121,\,\,\,f_{2}$$

$$21212\to212121,\,\,\,f_{1}$$

To make them satisfy instead \(\mathcal F(w,x)\mathcal F(x,w')+\mathcal F(w,y)\mathcal F (y,w')=0\), and to hence obtain the BGG differential, we can change all the \(\mathcal F(x,y)\) by a sign. These signs are not unique, but they do exist. We can compute them using the following code:

BGG.compute_signs()

{('', '1'): -1,
 ('', '2'): 1,
 ('2', '12'): -1,
 ('2', '21'): -1,
 ('1', '21'): -1,
 ('1', '12'): -1,
 ('12', '212'): -1,
 ('12', '121'): 1,
 ('21', '121'): -1,
 ('21', '212'): 1,
 ('121', '2121'): 1,
 ('121', '1212'): -1,
 ('212', '1212'): -1,
 ('212', '2121'): 1,
 ('2121', '12121'): -1,
 ('2121', '21212'): -1,
 ('1212', '21212'): -1,
 ('1212', '12121'): -1,
 ('21212', '212121'): -1,
 ('12121', '212121'): 1}